The construction

Some time ago, when playing around with the geometry-proof game Euclidea (not a sponsor), I stumbled upon an interesting pattern. It’s probably easiest to understand through a brief video.

Let’s first understand what exactly is the procedure followed by this construction. The setup is simple: we’re given a line \(\ell\) and a point \(P\). The construction begins by picking a point on \(\ell\), and drawing the circle centered at that point passing through \(P\). We will call the center point \(O_1\) and the circle \(\mathscr{C}_1\).

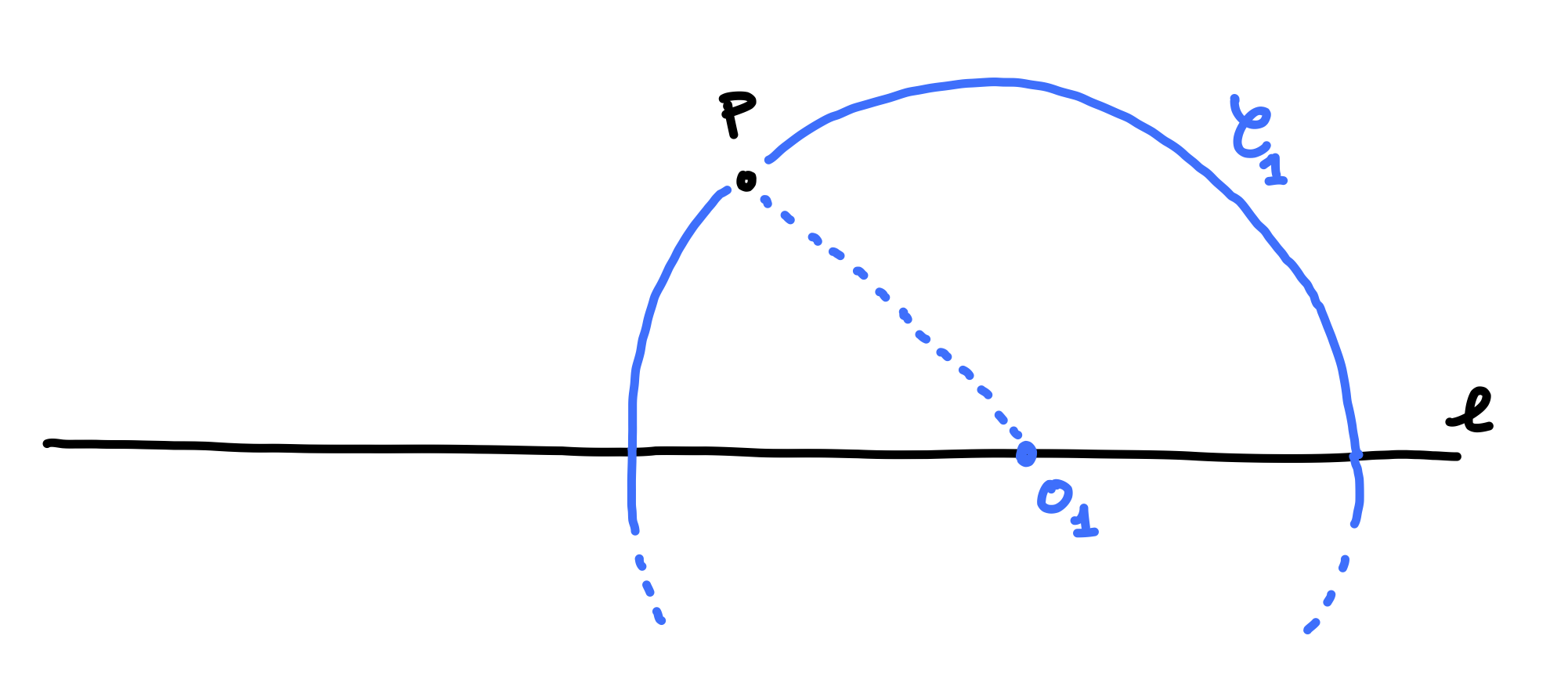
We then draw another circle through \(P\), this time centered at the intersection of the line with our previous cirlce \(\mathscr{C}_1\). But wait — the \(\mathscr{C}_1\) intersects \(\ell\) twice! Which intersection is our next center? From the video above, it’s clear that we pick the intersection point that lies “on the other side” of \(P\) from \(O_1\). We can make this formal drawing the perpendicular to \(\ell\) through \(P\). This perpendicular partitions the plane (i.e. the “paper” on which we are drawing our figure) into two half-planes, one of which contains \(O_1\) and exactly one of the intersections. We pick our next center \(O_2\) to be the intersection of \(\mathscr{C}_1\) and \(\ell\) in the half-plane not containing \(O_1\).

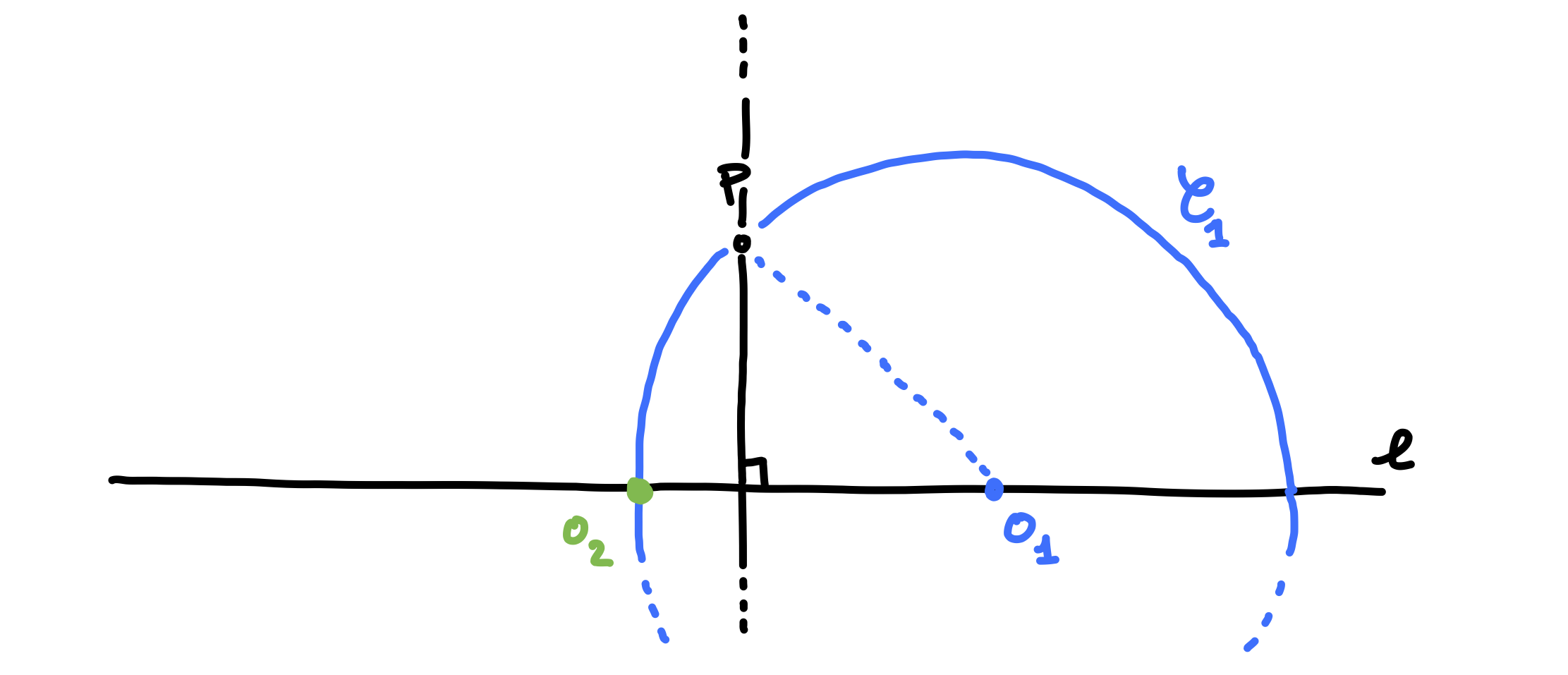
We pick \(O_3\) similarly.

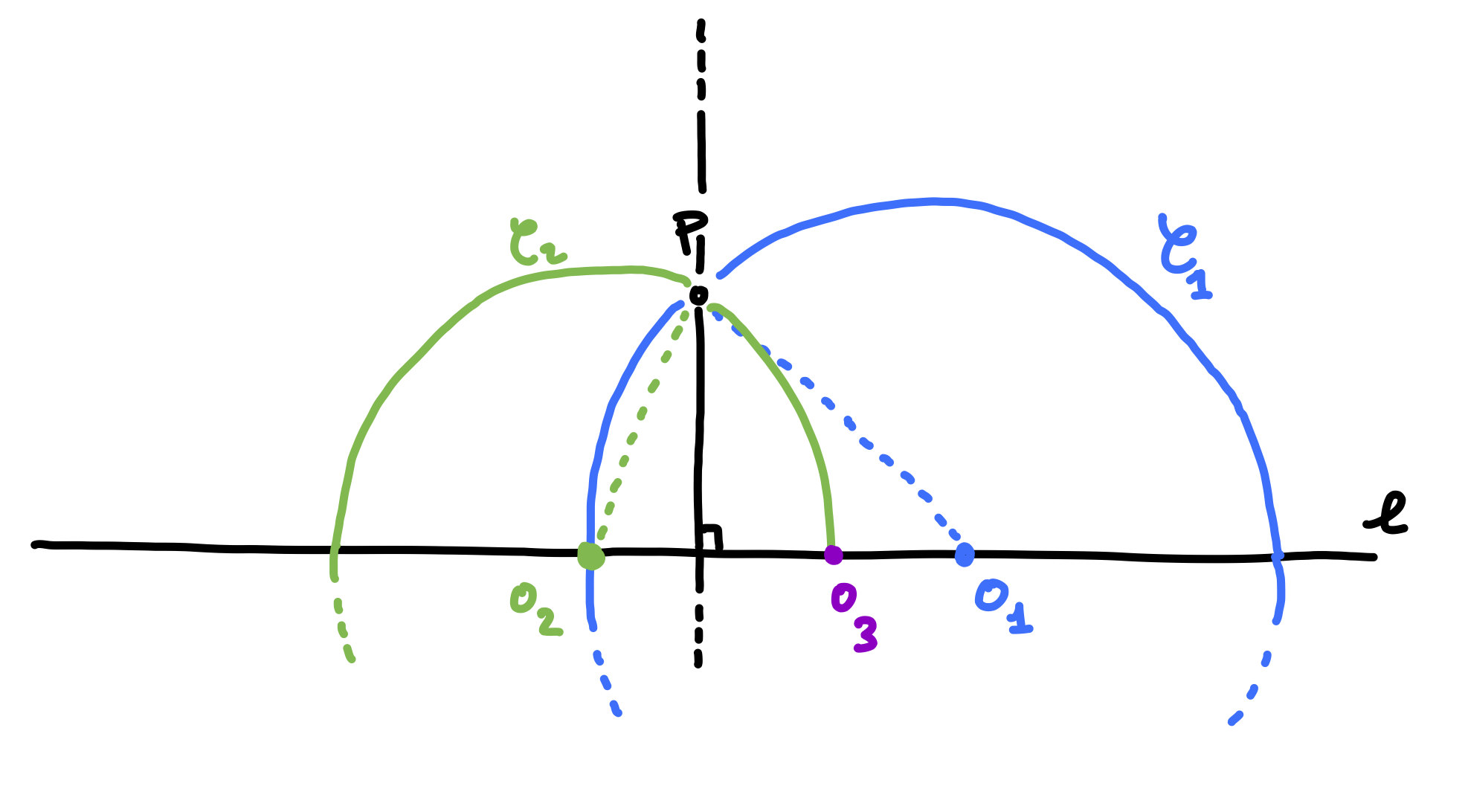
The construction proceeds in this way, picking new points \(O_i\) for \(i\) going to infinity. Below is an example of the construction up to \(O_{7}\).

Regardless of the position of \(O_1\), the constructed circles seem to converge pretty quickly (and we will try to understand how quickly). What exactly are they converging to? Upon further inspection, we see that the circle’s centers appear to converge to the vertices of an equilateral triangle with \(P\) as one vertex and the other two vertices on \(\ell\).

We will look at how you might prove this fact, in either one of two very different approaches. The first proof feels very elemental, relying (almost) exclusively on tools Euclid would have understood. However, it has the downside of being just a little long-winded. The second proof is unbelievably short and sweet in comparison.

The center-point proof

This problem actually bothered me for a while, and I would come back to it whenever I felt like thinking about some geometry. It took a few tries before I felt like I understood what was going on with each iteration of the construction, leading to what I’ll call the “center-point proof.” This first proof feels very elemental, relying (almost) exclusively on tools Euclid would have understood. It’s motivated by observing certain patterns in the construction.

We observed above that the vertices of a particular equilateral triangle seemed important. Let’s call these points \(L\) and \(R\). For convenience, we will also call \(C\) the base of the perpendicular of \(\ell\) through \(P\).

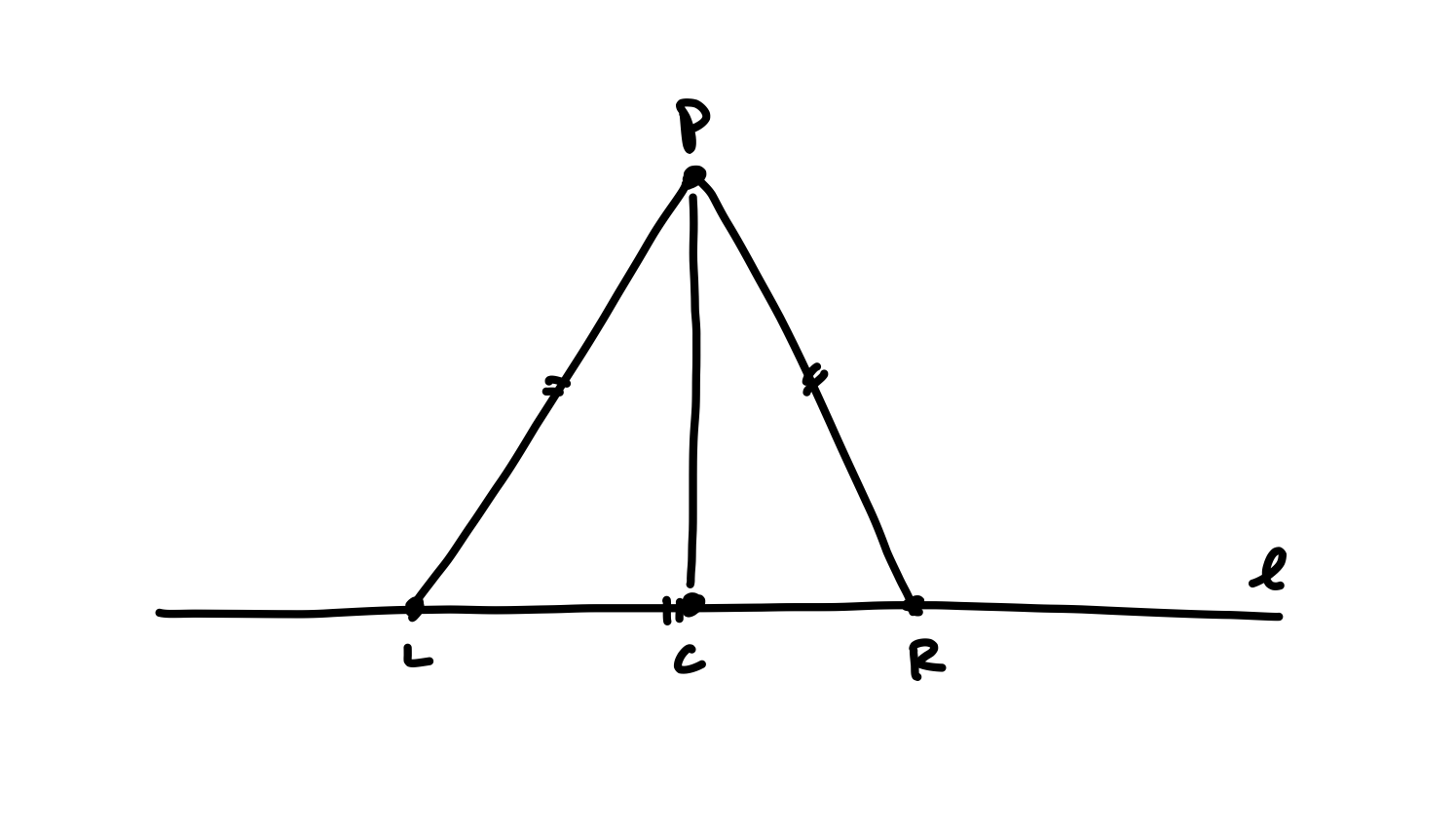
Let’s think about the different cases that can occur when we pick a point \(O_i\). For now, we will consider the case of where \(O_i\) is to the “right” of \(C\). Any results will essentially hold by symmetry for points to the “left” of \(C\). (Of course, there isn’t really such a thing as “right” or “left” in the construction, but I’ll use these terms as slightly sloppy short-hand, since it’s clear what they mean in context.)

The point \(O_i\) can be to the left of \(R\), the same as \(R\), or to the right of \(R\).

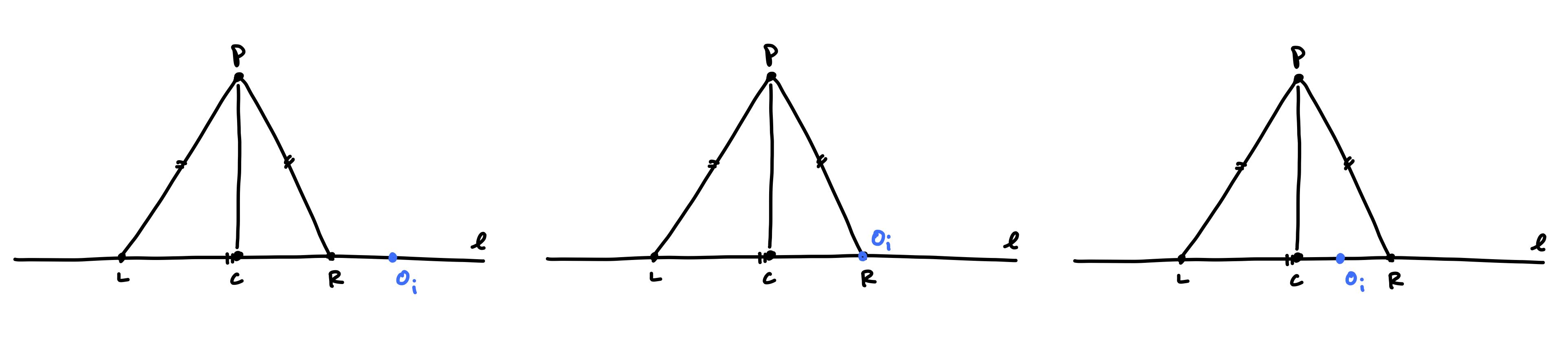
Note that if \(O_i = R\), then \(O_{i+1} = L\), and then \(O_{i+2} = R\), and so on… That is, \(R\) and \(L\) are fixed points of our construction — points that do not change as we iterate. (We will be more precise about this later.) So, the case \(O_i = R\) isn’t interesting to us.

What about when \(O_i\) is to the right of \(R\)? With just a little playing around, we can come up with the following.

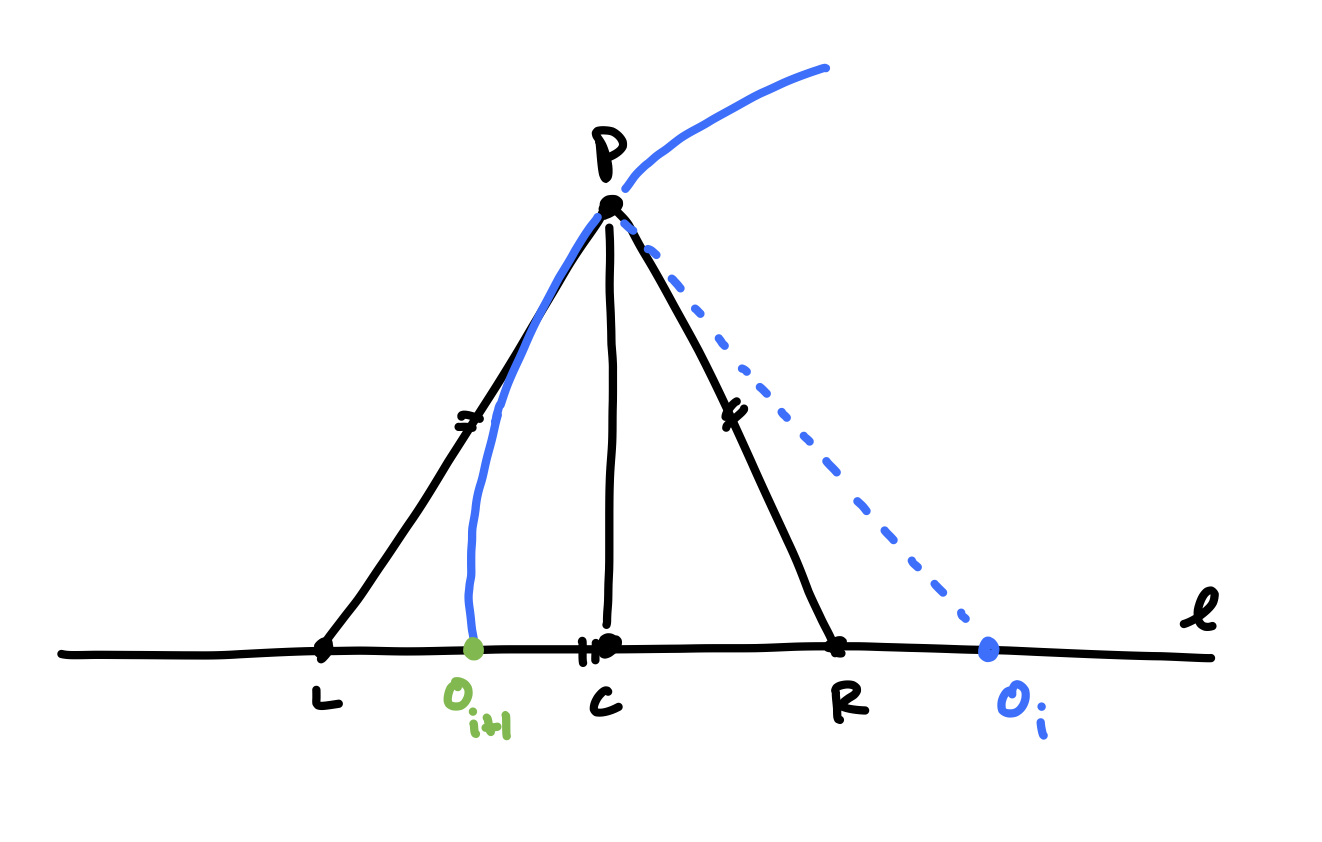
Lemma 1.1 If \(O_i\) is to the right of \(R\), then \(O_{i+1}\) is to the right of \(L\).

Proof : To prove this, we will show that \(\vert LO_i \vert > \vert O_{i+1} O_i \vert\). Our strategy will essentially be to express both quantities in terms of \(\vert LC \vert\) and \(\vert CO_i \vert\). The left-hand side is easy: \(\vert LO_i \vert = \vert LC \vert + \vert CO_i\vert\). The right-hand side is just a little trickier. First, note that by our construction \(\vert O_{i+1} O_i \vert = \vert P O_i \vert\), since both \(P\) and \(O_{i+1}\) lie on the same circle centered at \(O_i\). By the Pythagorean Theorem, \(\vert P O_i \vert = \sqrt{\vert PC \vert^2 + \vert CO_i \vert ^ 2}\). Since \(\triangle PLC\) is half of an equilateral triangle, we know that \(\vert PC \vert = \sqrt{3}\vert LC \vert\). Finally, this gives us that \(\vert O_{i+1}O_i \vert = \sqrt{3\vert LC \vert^2 + \vert CO_i \vert^2}\).

We now have an annoying square-root to deal with. Fortunately, since all our quantities are non-negative (being lengths of lines), we can equivalently show that \(\vert LO_i \vert^2 > \vert O_{i+1} O_i \vert^2.\) We can do this directly, as follows:

$$ \begin{align} \vert LO_i \vert^2 &= (\vert LC \vert + \vert CO_i \vert)^2\\ &= \vert LC \vert^2 + 2 \vert LC \vert \vert CO_i \vert + \vert CO_i \vert^2 \\ &> \vert LC \vert^2 + 2 \vert LC \vert\vert CR \vert + \vert CO_i \vert^2 \\ &= \vert LC \vert^2 + 2\vert LC \vert\vert LC \vert + \vert CO_i \vert^2 \\ &= 3\vert LC \vert^2 + \vert CO_i \vert^2 \\ &= \vert O_{i+1}O_i \vert^2. \end{align} $$

The inequality comes from our assumption that \(O_i\) is to the right of \(R\). The equality on the next line comes from our assumption that \(C\) lies halfway between \(L\) and \(R\) (since the perpendicular bisectors of the sides of an equilateral triangle are also its altitudes). This completes our proof. \(\blacksquare\)

As you might guess, we get the same kind of property when \(O_i\) is to the left of \(R\).

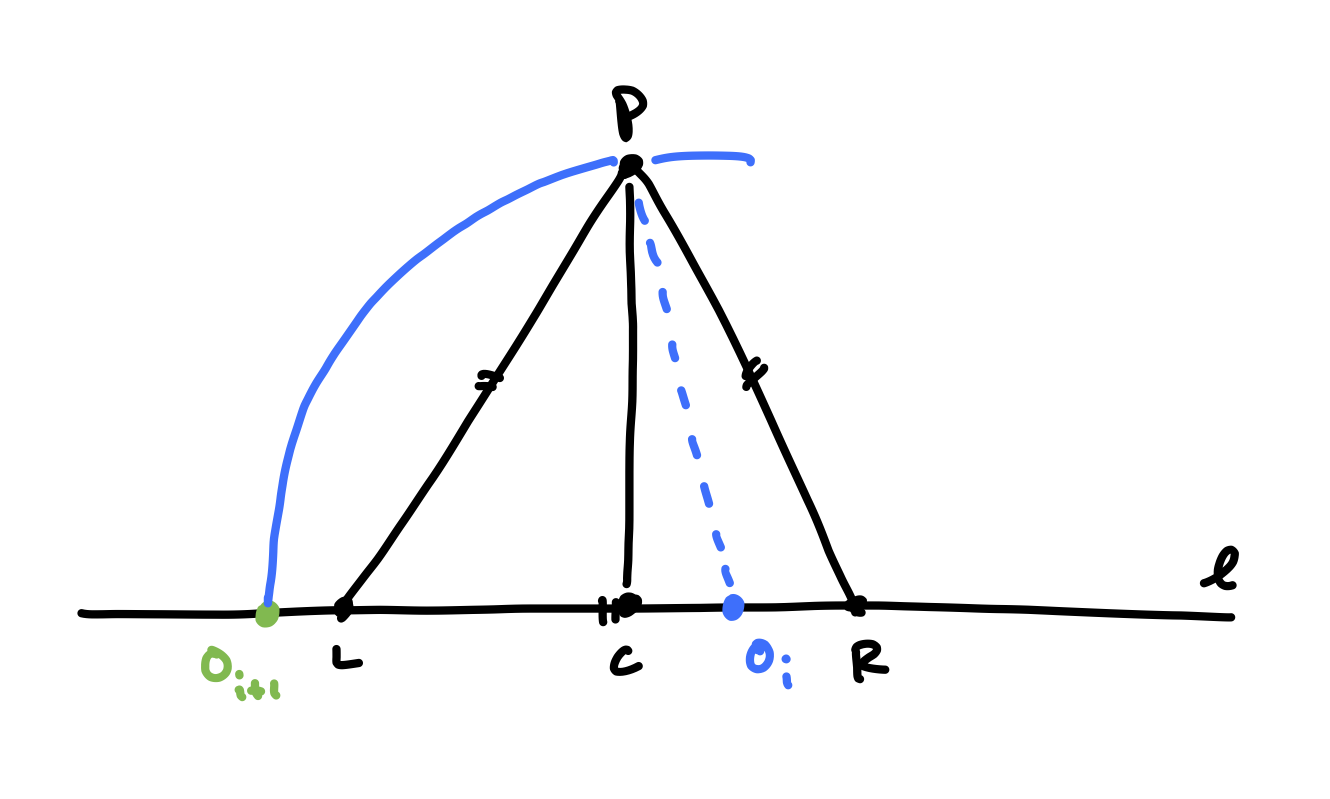
Lemma 1.2 If \(O_i\) is to the left of \(R\), then \(O_{i+1}\) is to the left of \(L\).

Proof: Taking a hint from our proof of Lemma 1.1 above, we want to show that \(\vert LO_i \vert < \vert O_{i+1} O_i \vert\). It turns out that the proof is almost identical. The one difference is that the inequality is reversed in the final calculation, since \(O_i\) is to the left of \(R\). \(\blacksquare\)

Now, we also want to reason about when \(O_i\) is to left of \(C\). With just a little thought, you can convince yourself that, by symmetry, we get the following facts — which for convenience we will group under the same lemmas.

Lemma 1.1 (\(L\) version) If \(O_i\) is to the left of \(L\), then \(O_{i+1}\) is to the left of \(R\).

Lemma 1.2 (\(L\) version) If \(O_i\) is to the right of \(L\), then \(O_{i+1}\) is to the right of \(R\).

We’ve looked one step ahead — seen what we can say about \(O_{i+1}\) given \(O_i\). Now let’s look two steps ahead, at \(O_{i+2}\). We hope that this helps us prove that the sequence of points \(O_i\), \(O_{i+2}\), \(O_{i+4}\), etc… approaches \(R\).

After some more thinking, the next observation seems a useful one to try to prove.

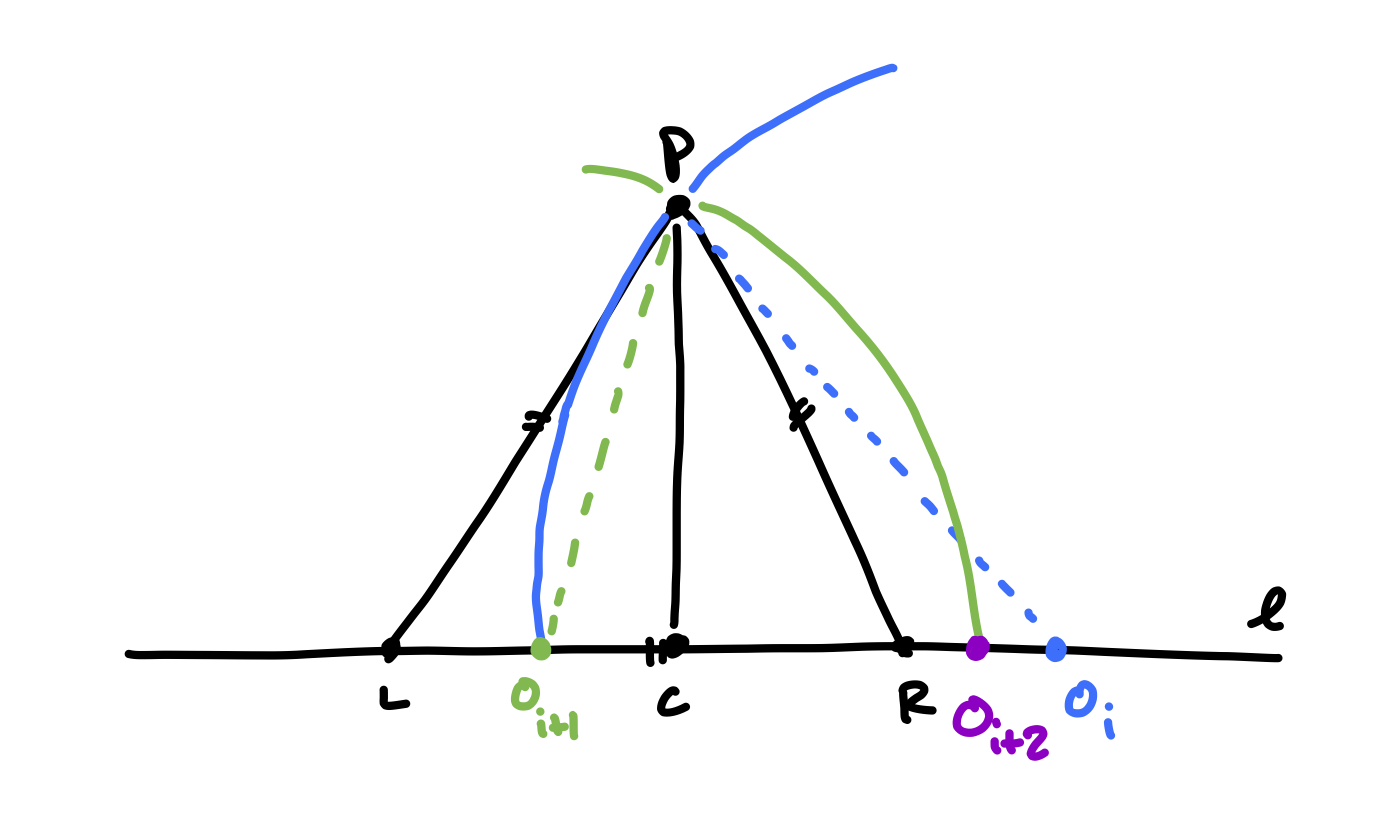
Proposition 2.1 If \(O_i\) is to the right of \(R\), then \(O_{i+2}\) is between \(R\) and \(O_i\).

Proof: By Lemma 1.1, \(O_{i+1}\) is to the right of \(L\). Then, by Lemma 2.2 (the “\(L\) version”), \(O_{i+2}\) is to the right of \(R\). So, we just have to show that \(O_{i+2}\) is to the left of \(O_i\). To do this, we will show that \(\vert O_{i+1} O_{i} \vert > \vert O_{i+1} O_{i+2} \vert\), as follows:

$$ \begin{align} \vert O_{i+1} O_{i} \vert = \vert P O_i \vert > \vert P R \vert = \vert P L \vert > \vert O_{i+1} P \vert = \vert O_{i+1} O_{i+2} \vert. \end{align} $$

The first and last equalities are true by our construction, the middle equality because \(\triangle PLR\) is equilateral, and the inequalities are easily verified — the first inequality, for example, by comparing the results of the Pythagorean theorem on \(\triangle PCO_i\) and \(\triangle PCR\), given that \(\vert CO_i \vert > \vert CR \vert\).

Unsurprisingly, we also have the following, with essentially the same proof.

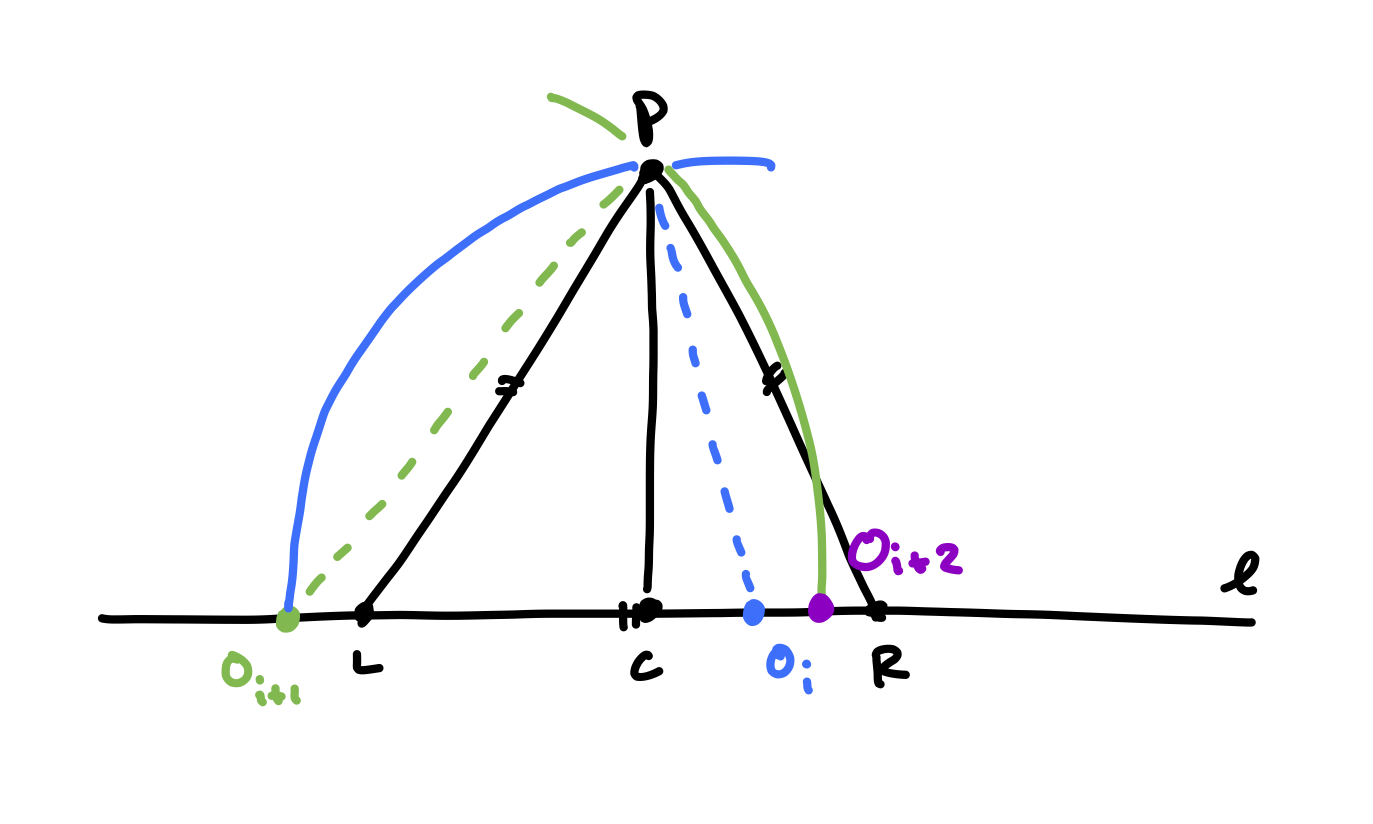
Proposition 2.2 If \(O_i\) is to the left of \(R\), then \(O_{i+2}\) is between \(R\) and \(O_i\).

But together, these propositions clearly imply a very useful statement. (Again, without loss of generality, we’re assuming \(O_i\) is to the right of \(C\).)

Theorem 3 \(O_{i+2}\) is between \(O_i\) and \(R\).

This is exciting! We should now have a picture in our mind of the points \(O_i\), \(O_{i+2}\), and so on, marching towards \(R\), getting closer and closer. Unfortunately, infinities are tricky, and there is one problem we still have to overcome: the points can get closer and closer to \(R\), without actually converging to \(R\) in the limit. For example, the distance between the current point an a “barrier” separated from \(R\) might be halved each time, à la Zeno’s paradox. Again, a picture is helpful here.

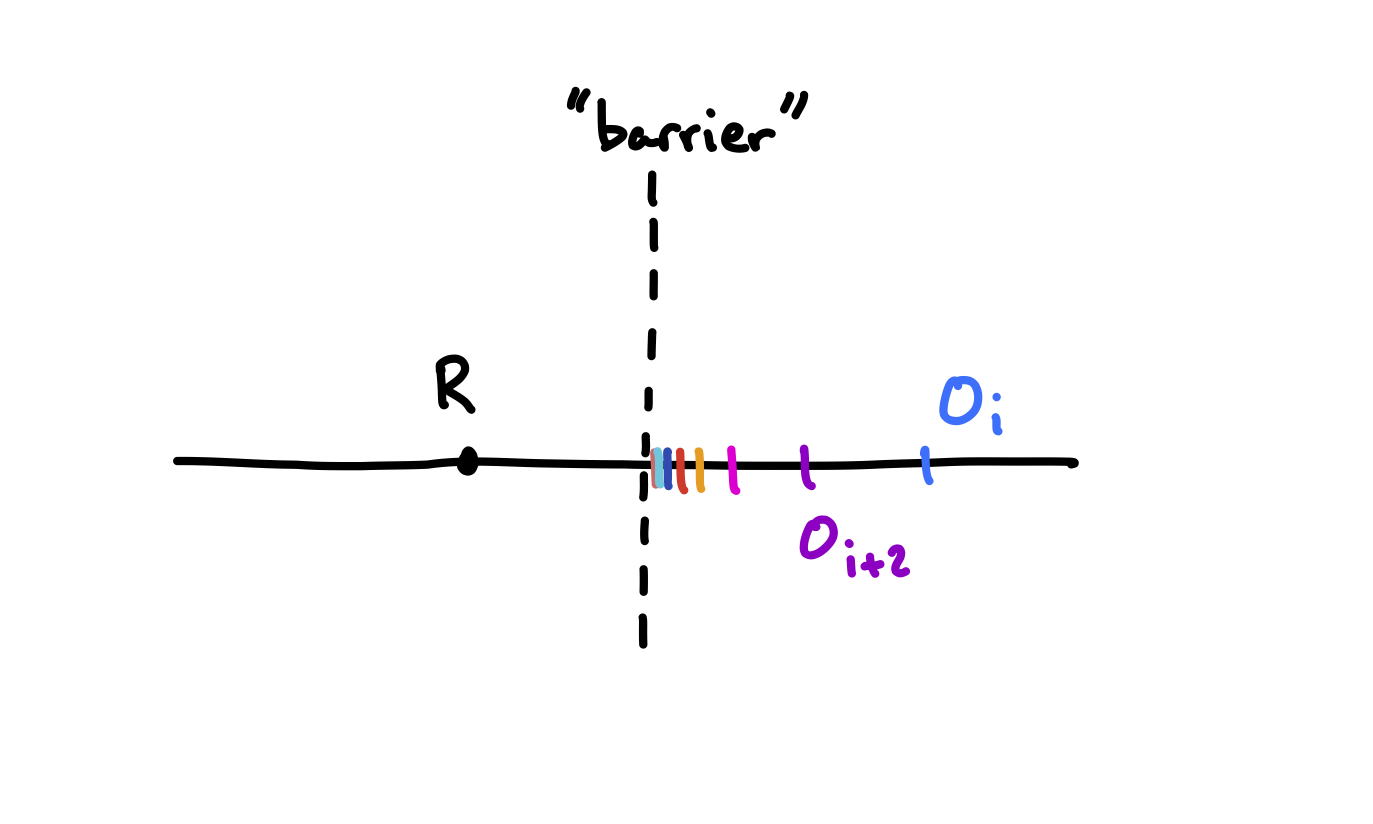
Nothing in our proofs above prevents this from being the case. To prove that it is not the case, we finally have to rely on one last bit of math Euclid would not have been familiar with: sequential continuity. Let’s call \(f\) the function that takes in a point \(O_i\) and gives back the point \(O_{i+2}\). I won’t prove it here, but \(f\) is continuous. To prove this, you could represent the points on \(\ell\) as real numbers (e.g. with \(C\) as the origin), find a closed-form expression for \(f\), and finally prove that the usual epsilon-delta definition of continuity holds. But this implies sequential continuity: if we call \(R'\) the point the sequence of points \(O_i\) approaches (which may or may not be \(R\)), then \(f(O_i)\) approaches \(f(R')\). But the sequences \(O_i\) and \(f(O_i)\) are just “shifts” of each other, and thus should approach the same point. That is, \(R' = f(R')\). Now, suppose that \(R'\) is not \(R\), and is instead some point to the right of \(R\). Our Theorem 3 above says that \(f(R')\) has to be between \(R'\) and \(R\) — i.e. not equal to \(R'\) (or \(R\)). This is a contradiction, since we just showed that \(R' = f(R')\). So, the point \(R'\) that the points \(O_i\) approach must in fact be \(R\).

And we are done (whew)! We have shown that the points on the right side of \(C\) approach \(R\), and the same argument could be repeated to show that the points to the left approach \(L\). The process was pretty long and meticulous, but did it have to be?

The contraction mapping proof

That Theorem 3 wasn’t sufficient was actually pointed out to me by a friend of mine, when I mentioned to him that I had finally solved the problem that had been on my mind for some time. We in fact gave up on the proof technique above — to my disappointment — decided just for fun to look for a new perspective on the problem. In large part due to my friend, we found one. (Only later did I come back to try and complete the center-point proof.) His intuition was two-fold: use the contraction mapping theorem, and look at angles being formed in the construction. Looking at angles is good idea, because then what we really want to show is that the angles at \(O_i\) from \(\ell\) to \(P\) — which we will call \(\theta_i\) — approach \(\frac{\pi}{3}\) (60 degrees).

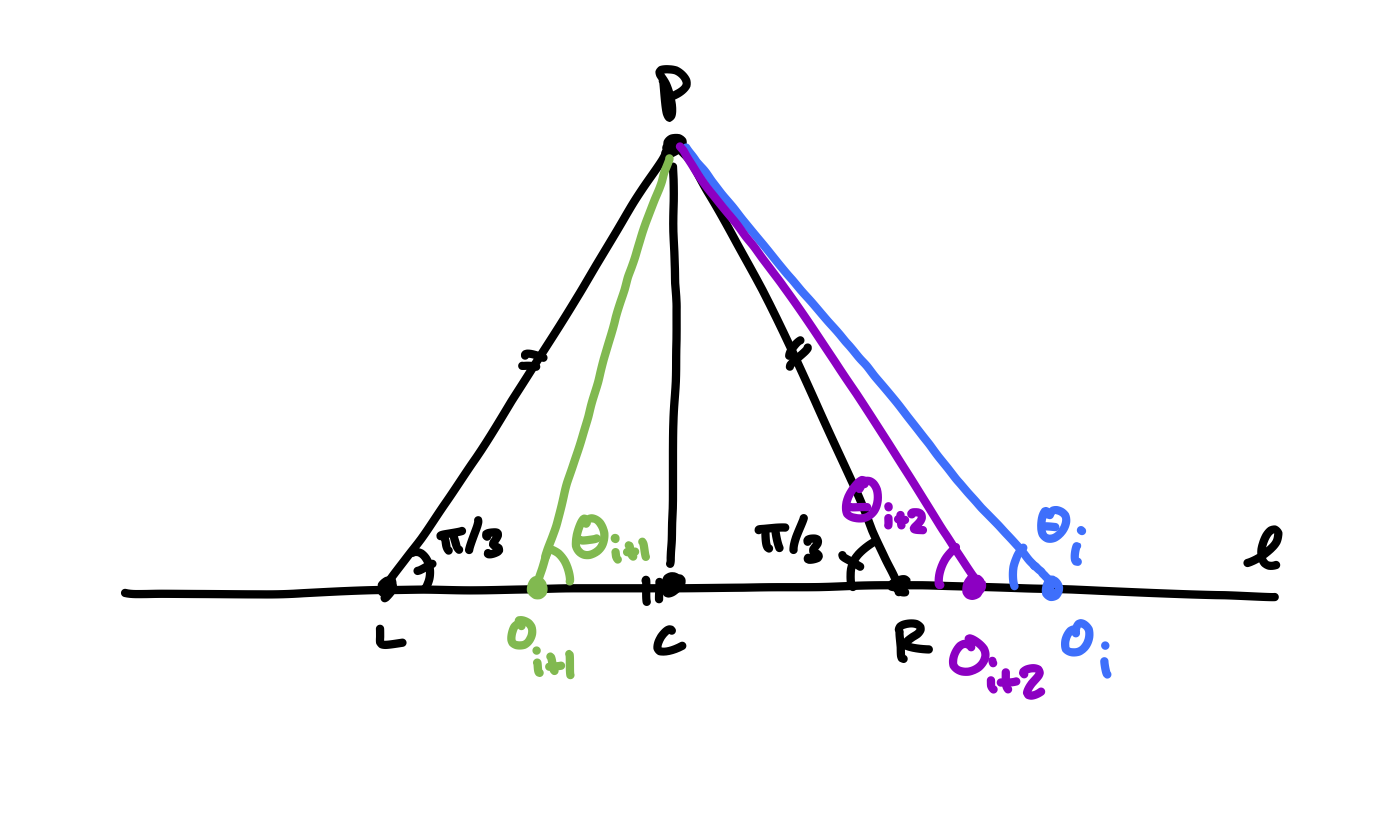
The contraction mapping theorem is generally a useful tool for showing such results. We first need to understand what is means for a function from real numbers to real numbers \(g: \mathbb{R} \rightarrow \mathbb{R}\) to be a “contraction mapping.” What this means is that there is some positive constant \(c < 1\) such that for any two real numbers \(x,y \in \mathbb{R}\), \(\vert g(x) - g(y) \vert < c \vert x - y \vert\). The contraction mapping theorem says that any contraction mapping \(g\) has a unique fixed point.

Our strategy is thus clear. Find the function that maps from the current angle \(\theta_i\) to \(\theta_{i+1}\), and show that it is a contraction mapping with fixed point \(\frac{\pi}{3}\). (Note that we in fact already know that this map, regardless of whether it is a contraction mapping, has this desired fixed point, but we still want to show it’s unique.)

Let’s look more carefully at the triangle \(\triangle P O_i O_{i+1}\).

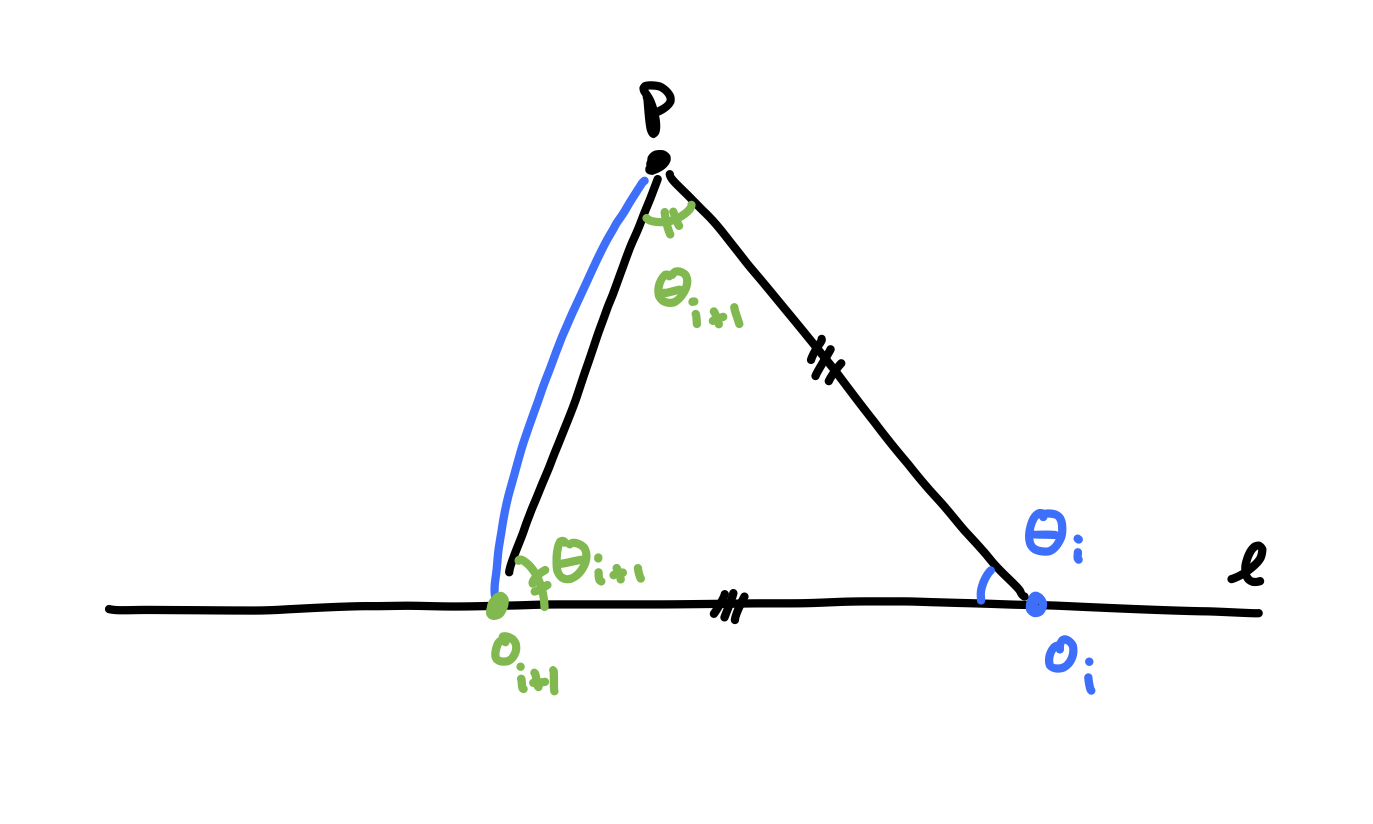
Since by construction \(\vert P O_i \vert = \vert O_{i+1} O_i \vert\), this triangle is isosceles. A result with the fancy name of pons asinorum tells us that the angles at the base of the triangle are equal; they’re both \(\theta_{i+1}\). Since the sum of all the angles in the triangle is \(\pi\), we get that \(g(\theta_i) = \theta_{i+1} = \frac{\pi-\theta_i}{2}\). We can immediately verify that \(g\) has the desired fixed point: \(g(\frac{\pi}{3}) = \frac{\pi}{3}\).

It thus remains to show that \(g\) is a contaction mapping. But this, in fact, is easy:

$$ \begin{align} \vert g(\alpha) - g(\beta) \vert = \left\vert \frac{\pi - \alpha}{2} - \frac{\pi-\beta}{2}\right\vert = \frac{1}{2} \vert \beta - \alpha \vert. \end{align} $$

And so, we’ve proven the convergence of our construction in essentially two lines: the definition of \(g\), and the proof that it’s a contraction mapping.

But how fast does it converge?

To be continued…