Counting Physical Laws
Introduction and Definitions
“How many physical laws are there for a system of n states?” This is a question I had while watching one of Leonard Susskind’s many great physics lectures accessible on on YouTube. It turns out to be a physics-y way of asking a combinatorial question, which I thought was pretty cool. When we pursue this idea far enough, we get to some interesting math, such as integer partitions, cycle type, and rencontres numbers.
First, I need to clarify what a “physical law” means in this context, and what a “system of \(n\) states” is. At the end of the day, these two can be described by a directed graph. We represent a “system of \(n\) states” by \(n\) nodes. A “physical law” for the system is a set of edges connecting these nodes, although, as we will see, with certain restrictions. For those unfamiliar with graphs, there isn’t too much machinery here, although an example may be helpful. You can think of “states” or “nodes” just as situations in which we can find a physical system. For example, an idealized coin on a table can be found in one of two states: heads or tails. We draw these diagramatically as circles.

A “physical law” describes how the state of a system changes from one point in time to the next. For example if we simply left the coin lying on the table, the next state will always be the same as the starting state. We represent these transitions with “directed edges,” i.e. arrows going from one state to another, giving us the following graph.
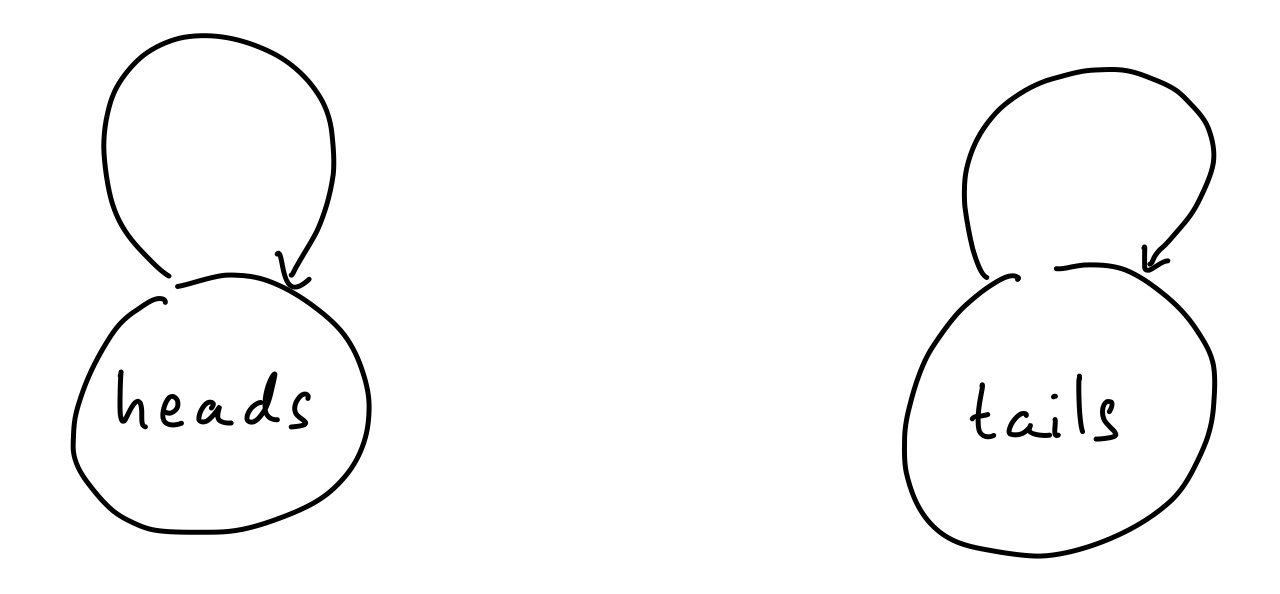
Or, we can imagine that we keep flipping the coin over, so that the state of the coin keeps switching: heads, tails, heads, tails, etc… This gives the graph below. (It’s worth noting that we are considering time as proceeding in discrete steps. If this seems strange, imagine for example that we observe the system — whether the coin is heads or tails — every three seconds.)

Built into the idea of a “physical law” is the fact that each state must have some next state. In terms of our graph, this means that each node must have an outgoing edge. We are now close to being able to precisely describe what we mean by counting the number of possible physical laws, but we will need some additional (well-motivated) constraints.
There are two interesting additional restrictions we may place on edges, motivated by what kinds of physical laws we want to consider.
The first is determinism. A classical physical system is deterministic. Given the state of a system, the laws specify what the next state will be; there is no randomness. This constrains each node (state) to have exactly one outgoing edge (exactly one next state). This contraint also gives us a well-defined counting problem: how many graphs exist with \(n\) nodes, such that each node has exactly one outgoing edge?
For now, we consider an additional constraint: the conservation of information. For our purposes, this principle amounts to, given the current state, being able to know what the previous state was (in addition to the next state). Another way of looking at it is that the system is “reversible.” Given the current state, we can run the system backwards in time to uncover the arbitrarily long history of the system. This gives a counterpart to the constraint above: each node must have exactly one incoming edge. Finally, we have the question we will tackle now: how many graphs exist with \(n\) nodes, such that each nodes has exactly one incoming edge and exactly one outgoing edge?
For the system of a coin on a table (or indeed any system of two states), we just have the possibilities from before — that is, switching between states, or staying in the starting state.
An easy result (labeled states)
A simple reading of this question has a very simple answer: \(n!\). To see this, just observe that a physical law is a permutation of \(n\) states; it associates each state \(i \in \{1,\ldots,n\}\) to a distinct “next state” \(j \in \{1,\ldots, n\}\). (I will admit that at first, this seemed a little strange to me, but it’s correct.)
Getting interesting: unlabeled states, or "kinds of laws"
The answer above is for the case where states are “labeled,” i.e. it differentiates between the two laws in the image below:

If we don’t really care about which state we call “1” and which we call “2,” our answer of \(n!\) isn’t what we want. This is also where our question of counting laws starts to become more interesting. We can also think of what we are asking for here as counting “kinds of physical laws,” or more precisely, counting graphs of \(n\) nodes with in-degree and out-degree one, up to relabeling of the nodes, i.e. up to graph isomorphism. Let’s look at the example for \(n=3\) states.

The key observation in solving this problem is that each “kind of physical law” is distinct a way of grouping \(n\) states into some number, let’s say \(m\), cycles. If we let the sizes of these cycles be \(\lambda_1, \ldots, \lambda_m\), then the only restriction is that \(\sum_{i=1}^m \lambda_i = n\). In other words, we can identify each “kind of law” with a way of writing \(n\) as the sum of positive integers, since each kind of law is described by the sizes of it’s cycles, which must add up to \(n\). The ways of writing a number \(n\) as the sum of positive integers are called integer partitions. So, the answer to the question “how many kinds of physical laws are there on \(n\) states” is: the number of integer partitions of \(n\). Unfortunately, this function — called the partition function — has no closed form, but it can be calculated via recurrence relations, or looked up for reasonably large \(n\) as A000041 in the OEIS (Online Encyclopedia of Integer Sequences).
How likely is each kind of law?
Equipt with the notion of a kind of law (law with unlabeled states), which groups together individual laws (laws with labeled states), we can ask how many of the labeled-state laws correspond to each kind of law. Another way of looking at this question is through the lens of assigning a probability to each kind of law, when we pick a physical law uniformly at random.
Let’s recall that each kind of physical law can be identified by cycle sizes \(\lambda_1, \ldots, \lambda_m\), and that a physical law is a permutation on \(n\) elements. It turns out that to say a physical law is of the kind \(\lambda := (\lambda_1, \ldots, \lambda_m)\) is to say that its cycle type is \(\lambda\). So, our question can be rephrased as: how many permutations are there for any given cycle type \(\lambda\)?
The answer isn’t obvious, and so we will prove it here. A perhaps slightly cleaner proof of this fact can be found here; nonetheless, I find the proof below a little more intuitive. However, it does require us to draw Young tableaux. As with graphs, this machinery isn’t too heavy — they turn out to be a useful way to represent integer partitions. You can think of a Young tableau as an upside-down staircase, where the length of the \(i\)th stair is \(\lambda_i\), making sure that the \(\lambda_i\)s are in sorted order.

(To be pedantic, a Young tableau is the drawing above with numbers placed in the boxes; otherwise, the drawing is called a “Young diagram”.)
So, given some cycle type \(\lambda\), we want to count the number of ways of filling the corresponding Young tableau, up to certain “symmetries” that we don’t care about. In particular, we don’t care about the following two symmetries. First is the order of rows of the same length. Let’s see an example.
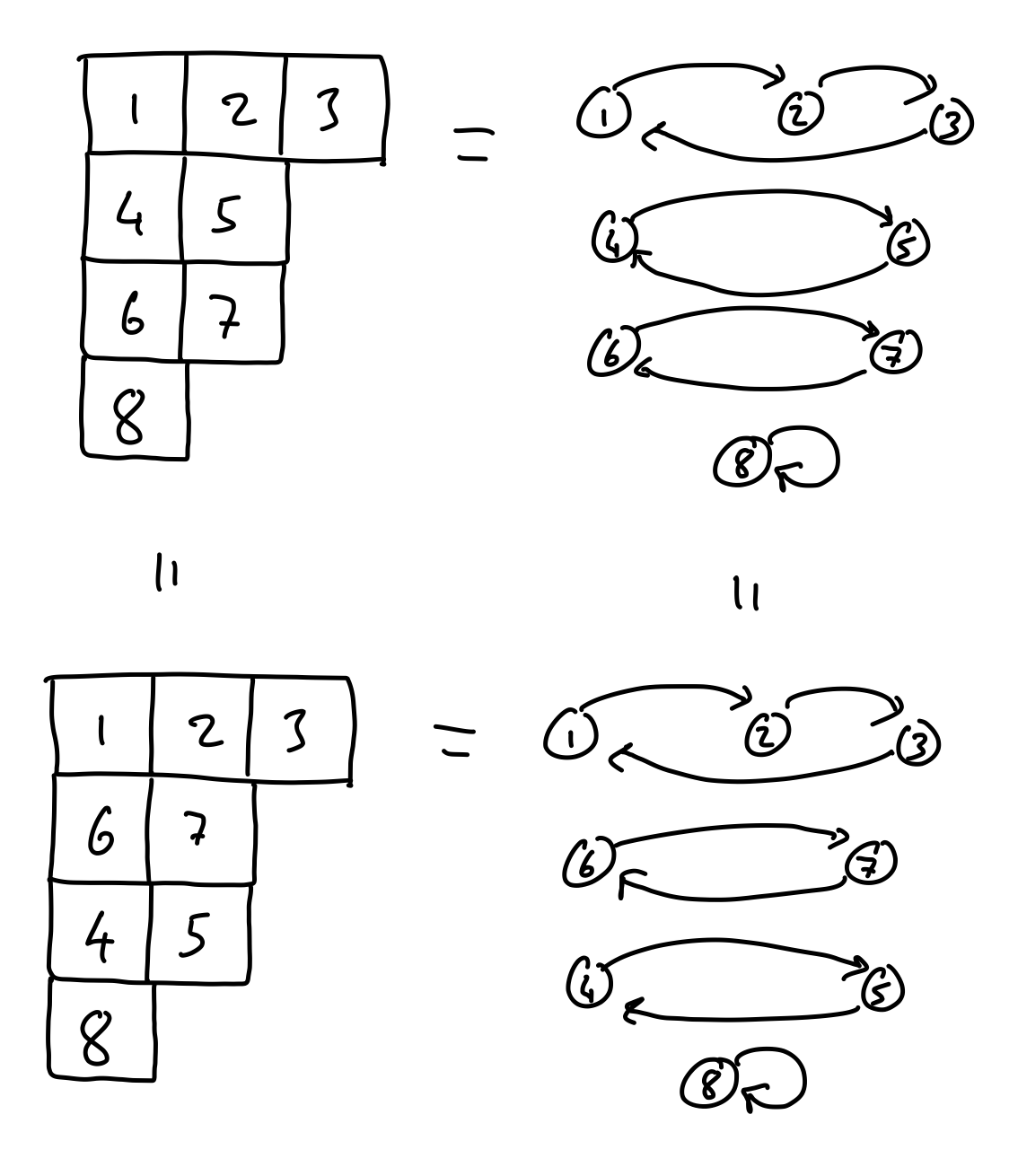
In the two examples above, we don’t care that the second and third rows are interchanged, since the two tableaux represent the same set of cycles.
The other symmetry has to do with the order in which the numbers are written within a single row. Since all we care about is representing a cycle, we can cycle the numbers within a row and still have an equivalent tableau. For example, the following two tableaux represent the same set of cycles.
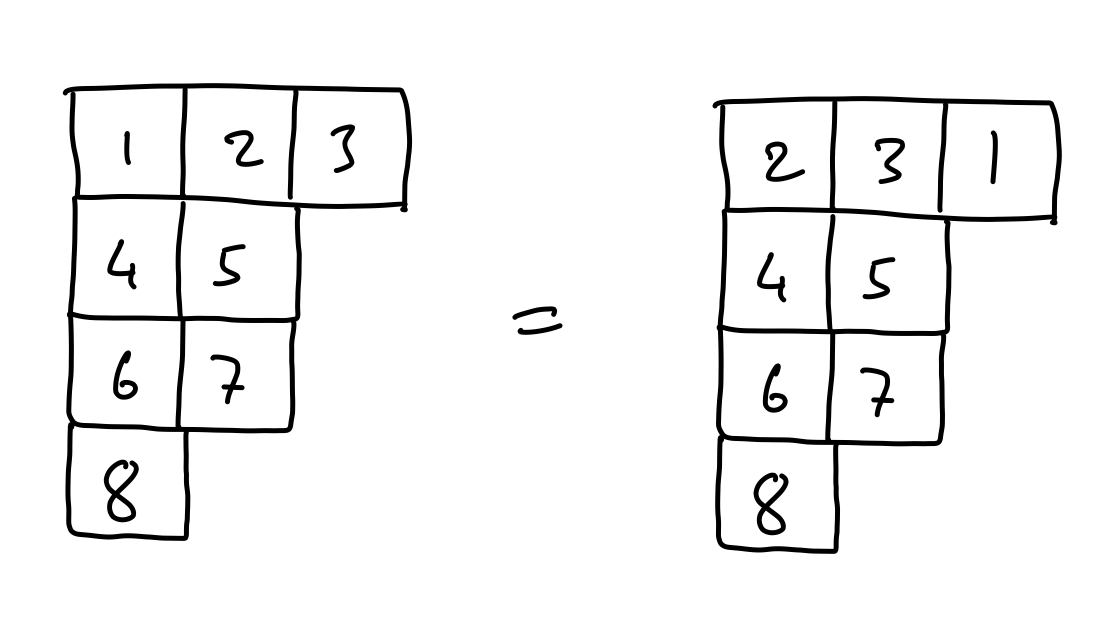
So, if we start with the total number of ways we can fill a Young tableau with \(n\) numbers, \(n!\), we just have to divide out the double-counting due to the symmetries we described above to get our answer! For the first — the switching of rows of the same length — we introduce the notation \(\mu(\lambda_i)\) to represent the “multiplicity” of \(\lambda_i\). In other words, \(\mu(\lambda_i)\) is the number of times \(\lambda_i\) appears in the cycle type \(\lambda\). We thus know that we must divide by a factor of \(\prod_{\text{distinct } \lambda_i} \mu(\lambda_i)!\).
To account for cycling within a row, we have to divide by number of possible cyclical “shifts,” which is just \(\lambda_i\) for row \(i\). The answer to our question of how many permutations (physical laws) have cycle type (kind of law) \(\lambda\) is therefore \(\frac{n!}{\prod_{\text{distinct } \lambda_i} \mu(\lambda_i)! \prod_{i=1}^m \lambda_i}\).
We saw that for \(n = 3\), the number of permutations for the three possible cycle types are 1, 3, and 2. Let’s look at \(n = 4\).

Here, we have cycle types (kinds of laws) of sizes 1, 6, 8, 3, and 6. If you are curious about the continuation of this sequence, you can turn to the sequence A181897 in OEIS. There is an interesting note on this page. It turns out that this sequence is a refinement of the rencontres numbers, which answer the question: how many permutations on \(n\) elements have \(k\) fixed points? That is to say, you can sum up elements of our sequence — permutations of a given cycle type — to get recontres numbers. For example, you can get the number of permutations of \(n = 5\) elements with one fixed point by adding up: (1) the number of permutations with two cycles of size two, and (2) the number of permutations with a cycle of size four.
What of the long term behavior of this sequence, for large \(n\)? That is, is there a kind of law that becomes more and more likely the bigger \(n\) gets? It turns out that for large \(n\), if you are picking between permutations uniformly, two kinds of laws emerge as the most likely by far (and one is as likely than the other in the limit). Let’s look at a graph of the counts of laws (permutations) of \(n = 50\) elements for each of the 204226 kinds of laws (cycle types).

The large spike on the right hand side actually corresponds to two cycle types, \(\lambda = (50)\) and \(\lambda = (1, 49)\), with counts of about \(6.08 \cdot 10^{62}\) and \(6.21 \cdot 10 ^{62}\), respectively. The order in which cycle types are place on the horizontal axis basically corresponds to the largest cycle size, increasing from left to right.
It’s easy to see qualitatively that \(\lambda = (1, n-1)\) and \(\lambda = (n)\) should be the two most common cycle types, by looking again at our equation for the number of permutations with a given cycle type: \(\frac{n!}{\prod_{\text{distinct } \lambda_i} \mu(\lambda_i)! \prod_{i=1}^m \lambda_i}\). To maximize this expression, we need to minimize the denominator. Since factorials grow very fast, we can heuristically restrict ourselves to having each \(\lambda_i\) (cycle size) in our cycle type be distinct, thus ensuring that \(\mu(\lambda_i) = 1\). We are thus left with the job of minimizing \(\prod_{i=1}^m \lambda_i\), the product of integers summing to \(n\). It’s easy to convince yourself that the optimum is achieved with \(\lambda = (1, n-1)\). (I haven’t proved this myself, but I don’t think it should be hard.) This gives us \(\frac{n!}{n-1} = n\cdot(n-2)!\) permutations of this cycle type, which is roughly \(\frac{n-1}{n} \approx 1\) times more that the \(\frac{n!}{n} = (n-1)!\) permutations of cycle type \(\lambda = (n)\).
I would like to make two final notes here. First, in the case \(n = 6\), there are 120 permutations both of cycle type \(\lambda = (6)\) and \(\lambda = (1,2,3)\). This is because both cycle types have the same product of cycle sizes. It turns out that this is rare — in fact, unique to the case \(n = 6\), if we restrict the cycle sizes to be unique. There is some interesting literature on when the sum of natural numbers equals their product, and the second link proves that for large \(n\), solutions have many 1’s (which means we have large \(\mu(\lambda_i)\) terms). The second note is the interesting shape of the graph above: a spike, a small region where permutations are roughly of equal probability, and a sharp drop-off. This pattern holds across all large enough values of \(n\) I have tried (which makes sense). It would be interesting to characterize how large the second “region” is.
A "corollary"
I would like to end with an interesting quantity we can calculate using our expression above for the number of permutations of a given cycle type: the number of ways to group \(n\) elements into groups of sizes \(\lambda = (\lambda_1, \ldots, \lambda_m)\). Let’s call this number \(g_n(\lambda)\). Then, the number of permutations of cycle type \(\lambda\) should be \(g_n(\lambda)\) times the number of ways to make a cycle of \(\lambda_i\) elements for each \(\lambda_i\) (i.e. for each group, how many different arangements into cycles are there). That is, the number of permutations of cycle type \(\lambda\) is \(g_n(\lambda) \prod_{i=1}^m (\lambda_i - 1)!\). Using our expression from before, we get \(g_n(\lambda) = \frac{n!}{\prod_{\text{distinct } \lambda_i} \mu(\lambda_i)! \prod_{i=1}^m \lambda_i \prod_{i=1}^m (\lambda_i - 1)!} = \frac{n!}{\prod_{\text{distinct } \lambda_i} \mu(\lambda_i)! \prod_{i=1}^m \lambda_i!}\).